সংজ্ঞা:
সংশ্লেষণ হলো দুটি চলকের মধ্যে সম্পর্ক পরিমাপের একটি পদ্ধতি। এটি একটি চলকের পরিবর্তনের সাথে অন্য চলকের পরিবর্তনের দিক এবং শক্তি বোঝায়।
মূল বৈশিষ্ট্য:
১. সংশ্লেষণের মান -1 থেকে +1-এর মধ্যে থাকে।
২. +1 ধনাত্মক সম্পর্ক বোঝায়, -1ঋণাত্মক সম্পর্ক বোঝায়, এবং 0 সম্পর্ক নেই বোঝায়।
৩. ধনাত্মক সংশ্লেষণে একটি চলকের বৃদ্ধি অন্যটির বৃদ্ধি ঘটায়।
৪. ঋণাত্মক সংশ্লেষণে একটি চলকের বৃদ্ধি অন্যটির হ্রাস ঘটায়।
পিয়ারসনের সংশ্লেষণ সহগ:
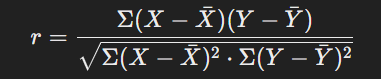
সংজ্ঞা:
নির্ভরণ হলো একটি চলকের ওপর অন্য একটি চলকের নির্ভরতার পরিমাণ নির্ধারণের পদ্ধতি। এটি ভবিষ্যদ্বাণী এবং মডেল তৈরিতে ব্যবহৃত হয়।
নির্ভরণ সমীকরণ:

মূল বৈশিষ্ট্য:
১. নির্ভরশীল চলকের মান পূর্বাভাস করার জন্য ব্যবহৃত হয়।
২. এটি কার্য-কারণ সম্পর্ক বোঝায়।
৩. ঢাল b স্বাধীন চলকের প্রতি নির্ভরশীল চলকের পরিবর্তনের হার প্রকাশ করে।
| বিষয় | সংশ্লেষণ | নির্ভরণ |
|---|---|---|
| উদ্দেশ্য | সম্পর্কের দিক এবং শক্তি নির্ধারণ। | নির্ভরতার পরিমাণ এবং পূর্বাভাস। |
| পরিমাপের সীমা | -1 থেকে +1 | কোনো নির্দিষ্ট সীমা নেই। |
| সম্পর্কের ধরন | পারস্পরিক সম্পর্ক। | কার্য-কারণ সম্পর্ক। |
| ফলাফল | সম্পর্কের সহগ। | নির্ভরণ সমীকরণ। |
স্ত্রীর বয়সের উপর স্বামীর বয়সের নির্ভরণ রেখার সমীকরণ = 5.57 +0.94y
জামালের বেতন বাড়ায় তার মাসিক খরচও বেড়ে গেল। তিনি তার খরচের গড় মান নির্ণয় করে দেখলেন বেতন বাড়ায় তার গড় খরচ বেড়ে যাচ্ছে। তার খরচের নির্ভরাঙ্কের মান 0.5।
সংজ্ঞা:
দ্বি-চলক তথ্য হলো এমন একটি ডেটাসেট, যা দুটি চলকের (variables) মান নিয়ে গঠিত এবং তাদের মধ্যে সম্পর্ক বিশ্লেষণ করতে ব্যবহৃত হয়।
উদাহরণ:
১. একজন ছাত্রের পড়ার সময় (ঘণ্টা) এবং পরীক্ষার ফলাফলের মধ্যে সম্পর্ক।
২. একটি কোম্পানির বিজ্ঞাপনের খরচ এবং বিক্রয় আয়ের মধ্যে সম্পর্ক।
প্রতিনিধিত্ব:
দ্বি-চলক তথ্য সাধারণত সমন্বিত জোড়া( X, Y)আকারে উপস্থাপিত হয়।
উদাহরণ:
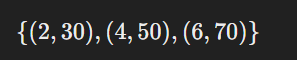
যেখানে এবং দুটি চলক।
সংজ্ঞা:
সংশ্লেষ হলো দুটি চলকের মধ্যে পারস্পরিক সম্পর্ক নির্ণয়ের পদ্ধতি। এটি নির্ধারণ করে একটি চলকের পরিবর্তনের সাথে অপর চলক কীভাবে এবং কতটা পরিবর্তিত হয়।
প্রকারভেদ:
১. ধনাত্মক সংশ্লেষণ (Positive Correlation):
একটি চলকের বৃদ্ধি অন্য চলকের বৃদ্ধি ঘটায়।
২. ঋণাত্মক সংশ্লেষণ (Negative Correlation):
একটি চলকের বৃদ্ধি অন্য চলকের হ্রাস ঘটায়।
৩. শূন্য সংশ্লেষণ (Zero Correlation):
চলকগুলোর মধ্যে কোনো সম্পর্ক নেই।
উদাহরণ:
সংজ্ঞা:
সংশ্লেষাংক হলো সংশ্লেষণের শক্তি এবং দিক নির্ণয়ের একটি পরিমাপ। এটি একটি চলকের পরিবর্তনের সাথে অন্য চলকের পরিবর্তনের মাত্রা নির্ধারণ করে।
গণনার সূত্র (পিয়ারসনের সংশ্লেষাংক):

উদাহরণ:
যদি কোনো ডেটাসেটের সংশ্লেষাংক r=0.8, তবে এটি একটি শক্তিশালী ধনাত্মক সম্পর্ক নির্দেশ করে।
| বিষয় | দ্বি-চলক তথ্য | সংশ্লেষ | সংশ্লেষাংক |
|---|---|---|---|
| সংজ্ঞা | দুটি চলকের মানের ডেটাসেট। | চলকগুলোর মধ্যে সম্পর্ক। | সম্পর্কের দিক এবং শক্তি। |
| প্রতিনিধিত্ব | (X, Y) আকারে। | ধনাত্মক, ঋণাত্মক বা শূন্য। | -1 থেকে +1-এর মধ্যে। |
| ব্যবহার | সম্পর্ক বিশ্লেষণের জন্য। | সম্পর্কের দিক নির্ধারণে। | সম্পর্কের শক্তি পরিমাপে। |
সংশ্লেষ (Correlation) হলো একটি পরিসংখ্যানিক পদ্ধতি যা দুটি ভেরিয়েবলের মধ্যে সম্পর্কের প্রকৃতি এবং তীব্রতা নির্ধারণ করে। সংশ্লেষ ডেটা বিশ্লেষণে গুরুত্বপূর্ণ ভূমিকা পালন করে, বিশেষ করে ভবিষ্যদ্বাণী বা পূর্বাভাস দেওয়ার ক্ষেত্রে।
সংশ্লেষকে প্রধানত তিনটি প্রকারে ভাগ করা হয়:
গ্রাফিক্যাল উপস্থাপনা: ডাটা পয়েন্টগুলো একটি উর্ধ্বমুখী সরল রেখায় থাকে।
গ্রাফিক্যাল উপস্থাপনা: ডাটা পয়েন্টগুলো একটি নিম্নমুখী সরল রেখায় থাকে।
গ্রাফিক্যাল উপস্থাপনা: ডাটা পয়েন্টগুলো এলোমেলোভাবে ছড়িয়ে থাকে।
সংশ্লেষ নির্ধারণের জন্য পিয়ারসন সংশ্লেষ সহগ (Pearson Correlation Coefficient) ব্যবহার করা হয়, যা r-এর মাধ্যমে প্রকাশ করা হয়। এর মান হতে পারে:
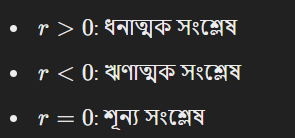
সংশ্লেষ ডেটা বিশ্লেষণে অত্যন্ত গুরুত্বপূর্ণ এবং এটি ধনাত্মক, ঋণাত্মক বা শূন্য হতে পারে। এটি বিভিন্ন ভেরিয়েবলের মধ্যে সম্পর্কের প্রকৃতি এবং তীব্রতা বুঝতে সাহায্য করে, যা সিদ্ধান্ত গ্রহণ এবং পূর্বাভাসের ক্ষেত্রে সহায়ক।
সংজ্ঞা:
বিক্ষেপ চিত্র হলো দ্বি-চলক ডেটা উপস্থাপনের একটি গ্রাফিক্যাল পদ্ধতি, যেখানে প্রতিটি ডেটা বিন্দু একটি চলকের (Independent Variable) মান এবং অপর চলকের (Dependent Variable) মানের সমন্বয় হিসেবে প্রদর্শিত হয়। এটি চলকগুলোর মধ্যকার সম্পর্কের ধরন (ধনাত্মক, ঋণাত্মক, বা শূন্য) বোঝাতে ব্যবহৃত হয়।
১. গ্রাফের উপাদান:
২. বিন্দুসমূহ:
প্রতিটি বিন্দু একটি নির্দিষ্ট X এবং Yমানের প্রতিনিধিত্ব করে।
৩. সম্পর্কের ধরন:
যদি বিক্ষেপ চিত্রের বিন্দুগুলো একটি ঊর্ধ্বমুখী রেখা বা প্রবণতা দেখায়, তাহলে এটি ধনাত্মক সংশ্লেষ নির্দেশ করে।
উদাহরণ:
একটি ছাত্রের পড়ার সময় বাড়লে পরীক্ষার নম্বর বৃদ্ধি পাওয়া।
বিক্ষেপ চিত্রে X (পড়ার সময়) বৃদ্ধি পেলে Y(পরীক্ষার নম্বর) ও বৃদ্ধি পায়।
যদি বিক্ষেপ চিত্রের বিন্দুগুলো একটি নিম্নমুখী রেখা বা প্রবণতা দেখায়, তাহলে এটি ঋণাত্মক সংশ্লেষ নির্দেশ করে।
উদাহরণ:
পণ্যের দাম বাড়লে বিক্রয় কমে যায়।
বিক্ষেপ চিত্রে X(মূল্য) বৃদ্ধি পেলে Y (বিক্রয়) হ্রাস পায়।
যদি বিক্ষেপ চিত্রে বিন্দুগুলো এলোমেলোভাবে ছড়ানো থাকে এবং কোনো নির্দিষ্ট প্যাটার্ন না দেখা যায়, তাহলে এটি শূন্য সংশ্লেষ নির্দেশ করে।
উদাহরণ:
একটি ছাত্রের পছন্দের খাবার এবং তার পরীক্ষার নম্বরের মধ্যে সম্পর্ক।
১. দৃষ্টিগ্রাহ্য বিশ্লেষণ:
বিক্ষেপ চিত্র চলকগুলোর সম্পর্ক সহজেই চিত্রায়িত করে এবং সংশ্লেষের প্রাথমিক ধারণা প্রদান করে।
২. সম্পর্কের প্রকৃতি:
এটি চলকগুলোর সম্পর্কের ধরণ (ধনাত্মক, ঋণাত্মক বা শূন্য) নির্ধারণ করতে সহায়ক।
একটি কোম্পানির বিজ্ঞাপনের খরচ (X) এবং বিক্রয় (Y) এর ডেটা:
X = [10, 20, 30, 40, 50], Y = [15, 25, 35, 45, 55]
বিক্ষেপ চিত্রে বিন্দুগুলো ঊর্ধ্বমুখী হওয়ায় এটি একটি ধনাত্মক সম্পর্ক নির্দেশ করে। বিজ্ঞাপনের খরচ বাড়ানোর সাথে সাথে বিক্রয় বৃদ্ধি পাচ্ছে।
এভাবে বিক্ষেপ চিত্র চলকগুলোর সম্পর্ক বিশ্লেষণ এবং ভবিষ্যৎ সিদ্ধান্ত গ্রহণে সহায়ক।
সংশ্লেষাঙ্ক হলো একটি পরিসংখ্যানগত পরিমাপ, যা দুটি চলকের (Variables) মধ্যে পারস্পরিক সম্পর্কের মাত্রা ও দিক নির্দেশ করে। এটি সাধারণত দুটি পরিমাণগত চলকের মধ্যে একটি রেখীয় সম্পর্কের (Linear Relationship) শক্তি এবং দিক নির্ধারণে ব্যবহৃত হয়।
সংশ্লেষাঙ্কের মান সাধারণত −1 থেকে +1-এর মধ্যে থাকে।

সূত্র:

ধরা যাক, একটি স্কুলে ছাত্রদের পড়াশোনার সময় এবং পরীক্ষার নম্বরের মধ্যে সম্পর্ক বিশ্লেষণ করতে হবে। সংশ্লেষাঙ্ক ব্যবহার করে দেখা যায়:
সংশ্লেষাঙ্ক একটি গুরুত্বপূর্ণ পরিসংখ্যানগত পদ্ধতি, যা বিভিন্ন ক্ষেত্র যেমন গবেষণা, ব্যবসা, স্বাস্থ্য, ও শিক্ষা ক্ষেত্রে সম্পর্ক বিশ্লেষণে ব্যবহৃত হয়। এটি দুই চলকের মধ্যকার সম্পর্কের দিক ও শক্তি নির্ধারণে কার্যকর।
ক্রম সংশ্লেষ (Sequence Summation) হলো কোনো ক্রম (যেমন, সংখ্যা, অক্ষর বা বস্তু) এর উপাদানগুলো যোগ করার প্রক্রিয়া। এটি গণিতের একটি গুরুত্বপূর্ণ ধারণা, যা বিভিন্ন সমস্যা সমাধানে ব্যবহৃত হয়। ক্রম সংশ্লেষের জন্য কিছু নির্দিষ্ট সূত্র রয়েছে, যা গণনাকে সহজ করে।

কিছু গুরুত্বপূর্ণ ক্রম সংশ্লেষের সূত্র নিচে উদ্ভাবনসহ উল্লেখ করা হলো:


এটি প্রমাণ করা যায়:
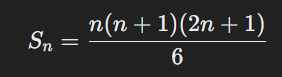
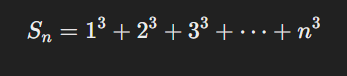
এটি প্রমাণ করা যায়:
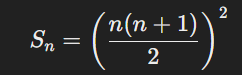
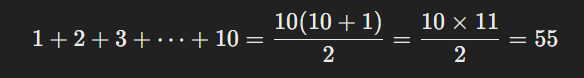
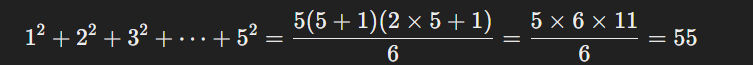
ক্রম সংশ্লেষ হলো ক্রমের উপাদানগুলোর যোগফল নির্ণয় প্রক্রিয়া। প্রাকৃতিক সংখ্যার যোগফল, বর্গের যোগফল এবং ঘনের যোগফলের জন্য নির্দিষ্ট সূত্র রয়েছে, যা গণনাকে সহজ ও দ্রুততর করে।
সংজ্ঞা:
নির্ভরণ হলো দুটি চলকের (variables) মধ্যে কার্য-কারণ সম্পর্ক নির্ধারণের পদ্ধতি। এটি একটি চলকের মানের ভিত্তিতে অন্য চলকের মান পূর্বাভাস করার জন্য ব্যবহৃত হয়।
উদ্দেশ্য:
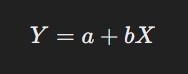
নির্ভরণ সমীকরণ:
যেখানে,

উদাহরণ:
একটি দোকানের বিজ্ঞাপনের খরচ (X) এবং বিক্রয় (Y) এর মধ্যে সম্পর্ক নির্ধারণ। বিজ্ঞাপনের খরচ বাড়ালে বিক্রয় কতটা বাড়বে তা নির্ভরণ দ্বারা বোঝা যায়।
সংজ্ঞা:
নির্ভরাংক হলো নির্ভরণ সমীকরণের ঢাল (Slope), যা স্বাধীন চলকের পরিবর্তনের সাথে নির্ভরশীল চলকের পরিবর্তনের পরিমাণ প্রকাশ করে।
গুরুত্বপূর্ণ বৈশিষ্ট্য:
১. নির্ভরাংক b একটি চলকের প্রতি অন্য চলকের নির্ভরতাকে পরিমাপ করে।
২. এটি একটি ধনাত্মক বা ঋণাত্মক মান হতে পারে:
নির্ণয়ের সূত্র:
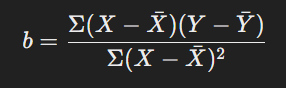
নির্ভরণ:
১. ভবিষ্যদ্বাণী (Prediction):
বিজ্ঞাপনের খরচের ভিত্তিতে বিক্রয় পূর্বাভাস।
২. মডেলিং:
আবহাওয়ার পূর্বাভাস বা পণ্যের চাহিদার পূর্বাভাস।
৩. ব্যবসায়িক সিদ্ধান্ত:
উৎপাদন খরচ ও মুনাফার সম্পর্ক বিশ্লেষণ।
নির্ভরাংক:
১. পরিবর্তনের হার বিশ্লেষণ:
বিক্রয় বৃদ্ধি বা হ্রাসের পরিমাণ বোঝা।
২. কার্য-কারণ সম্পর্ক নির্ধারণ:
স্বাধীন চলক কতটা প্রভাব ফেলে তা বিশ্লেষণ।
| বিষয় | নির্ভরণ (Regression) | নির্ভরাংক (Regression Coefficient) |
|---|---|---|
| সংজ্ঞা | নির্ভরশীল ও স্বাধীন চলকের মধ্যে সম্পর্ক। | স্বাধীন চলকের প্রতি নির্ভরশীল চলকের পরিবর্তনের হার। |
| উদ্দেশ্য | ভবিষ্যদ্বাণী ও সম্পর্ক নির্ধারণ। | সম্পর্কের পরিমাণ পরিমাপ। |
| ফলাফল | নির্ভরণ সমীকরণ। | একটি ধনাত্মক বা ঋণাত্মক মান। |
নির্ভরণ (Dependence)
নির্ভরণ হলো এমন একটি সম্পর্ক যেখানে একটি ভেরিয়েবলের মান অন্য একটি ভেরিয়েবলের উপর নির্ভর করে। এটি গণিত, বিজ্ঞান, প্রযুক্তি, এবং পরিসংখ্যানসহ বিভিন্ন ক্ষেত্রে গুরুত্বপূর্ণ ধারণা। নির্ভরণের প্রকৃতি অনুযায়ী এটি বিভিন্ন ভাগে বিভক্ত।
উদাহরণ:
উদাহরণ:
উদাহরণ:
উদাহরণ:
উদাহরণ:
উদাহরণ:
উদাহরণ:
উদাহরণ:

নির্ভরণ বিভিন্ন প্রকারে শ্রেণীবদ্ধ করা যায় যেমন সরল, যৌগিক, রৈখিক, অরৈখিক, পরস্পর, কার্যকর, সম্ভাব্য, শর্তাধীন, সম্পূর্ণ এবং আংশিক নির্ভরণ। নির্ভরণের এই ভিন্ন ভিন্ন প্রকার বাস্তব জীবনে বিভিন্ন পরিস্থিতি বিশ্লেষণ ও সমস্যার সমাধানে গুরুত্বপূর্ণ ভূমিকা পালন করে।
নির্ভরণ বা সংশ্লেষ (Correlation) পরিসংখ্যান এবং ডেটা বিশ্লেষণের একটি গুরুত্বপূর্ণ পদ্ধতি, যা ভেরিয়েবলগুলোর মধ্যে সম্পর্ক নির্ধারণে ব্যবহৃত হয়। এটি বিভিন্ন ক্ষেত্রে সিদ্ধান্ত গ্রহণ, গবেষণা এবং পূর্বাভাসে গুরুত্বপূর্ণ ভূমিকা পালন করে।
নির্ভরণ ভেরিয়েবলের সম্পর্ক বিশ্লেষণ ও সিদ্ধান্ত গ্রহণের একটি শক্তিশালী পদ্ধতি। এটি গবেষণা, ডেটা বিশ্লেষণ, পূর্বাভাস এবং ব্যবসায়িক সিদ্ধান্ত গ্রহণে বহুল ব্যবহৃত হয়। নির্ভরণ সঠিক সম্পর্ক নির্ধারণের মাধ্যমে জটিল সমস্যার সমাধান সহজ করে তোলে।
নির্ভরাঙ্ক হলো পরিসংখ্যানের একটি গুরুত্বপূর্ণ মাপ, যা দুটি চলকের (Variables) মধ্যে নির্ভরশীল সম্পর্কের মাত্রা ও দিক নির্দেশ করে। এটি মূলত একটি চলকের মান পরিবর্তনের ফলে অন্য চলকের মান কীভাবে পরিবর্তিত হবে তা নির্ধারণ করতে ব্যবহৃত হয়।

দুটি নির্ভরাঙ্কের গুণফল সংশ্লেষাঙ্কের বর্গের সমান:
এখানে r হলো সংশ্লেষাঙ্ক।
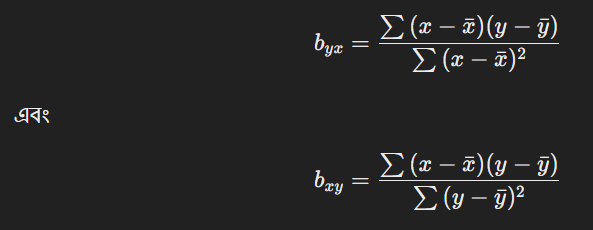
ধরা যাক, একজন ব্যবসায়ী বিজ্ঞাপনের জন্য ব্যয় (x) এবং বিক্রয়ের পরিমাণ (y)এর মধ্যে সম্পর্ক নির্ধারণ করতে চান। নির্ভরাঙ্কের মান পাওয়া গেলে এর অর্থ হলো, বিজ্ঞাপনে প্রতি ১ লক্ষ টাকা ব্যয় বাড়ালে বিক্রয়ের পরিমাণ ২.৫ লক্ষ টাকা বাড়বে।
নির্ভরাঙ্ক হল দুটি চলকের মধ্যে সম্পর্কের দিক ও মাত্রা বোঝার জন্য অত্যন্ত কার্যকর একটি পরিসংখ্যানগত টুল। এটি ভবিষ্যদ্বাণী এবং সম্পর্ক বিশ্লেষণের জন্য বিভিন্ন ক্ষেত্রে, যেমন ব্যবসা, অর্থনীতি, এবং গবেষণায় ব্যাপকভাবে ব্যবহৃত হয়।
নির্ভরণ সমীকরণ এবং নির্ভরণ রেখা (Equation of Line and Line Equation) গণিতের গুরুত্বপূর্ণ ধারণা, যা জ্যামিতি ও বিশ্লেষণমূলক জ্যামিতিতে ব্যাপকভাবে ব্যবহৃত হয়। এখানে নির্ভরণ সমীকরণ এবং নির্ভরণ রেখার বিস্তারিত আলোচনা দেওয়া হলো।
নির্ভরণ সমীকরণ হলো একটি রেখার গাণিতিক উপস্থাপন, যা নির্দিষ্ট বিন্দু বা শর্ত পূরণ করে। দুই মাত্রার 2D সমতলে একটি রেখা x এবং \y-এর মধ্যে সম্পর্ক স্থাপন করে। এটি সাধারণত দুটি রূপে প্রকাশ করা হয়:
এখানে,
Ax + By + C = 0
এখানে, A, B, এবং C হলো ধ্রুবক (constants)।
নির্ভরণ রেখা হলো একটি সরলরেখা, যা নির্ভর করে সমীকরণের ধ্রুবক গুণাগুণের উপর। এটি সমতলে xও y-এর সম্পর্ক প্রদর্শন করে। রেখা বিভিন্ন শর্তে ভিন্ন রূপে প্রকাশিত হয়:
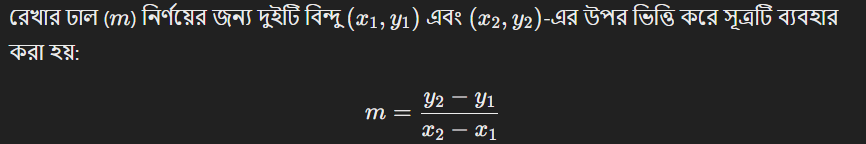
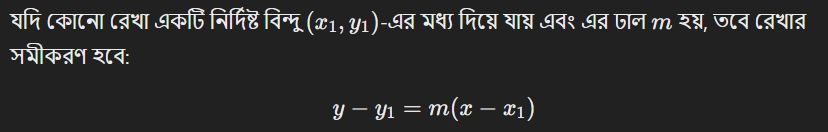
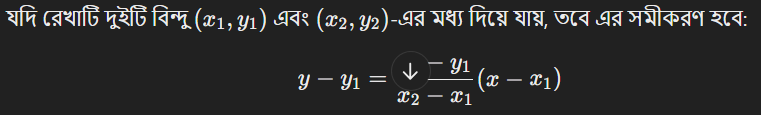
যদি রেখাটি অনুভূমিক হয়, তবে y=c, যেখানে c হলো y-অক্ষের উপর রেখার উচ্চতা।
যদি রেখাটি উল্লম্ব হয়, তবে x = k, যেখানে k হলো x-অক্ষের উপর রেখার স্থান।
ধরা যাক, একটি রেখার ঢাল m = 2 এবং y-অক্ষের উপর ছেদ বিন্দু c = -3। রেখার সমীকরণ হবে:
দুটি বিন্দু \(1, 2) এবং (3, 6) -এর মধ্য দিয়ে যাওয়া রেখার সমীকরণ নির্ণয় করতে:
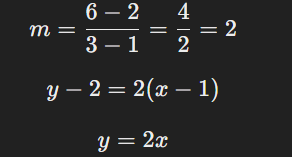
নির্ভরণ সমীকরণ এবং নির্ভরণ রেখা জ্যামিতি ও বিশ্লেষণমূলক গণিতের ভিত্তি। এটি বিভিন্ন রূপে প্রকাশিত হয়, যেমন ঢাল-কেটে রূপ, সাধারণ রূপ, এবং বিন্দু-ঢাল রূপ। রেখার ঢাল, বিন্দু, এবং অবস্থানের ভিত্তিতে এর সমীকরণ নির্ধারণ করা হয়।
Read more